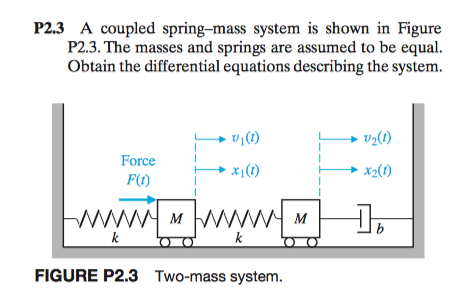
Coupled Spring Mass System
Coupled spring mass system. A Coupled Spring-Mass System. Four Masses coupled with Five spring without Damping. Sys matlabFunction ODE Vars t Y K f m1 m2.
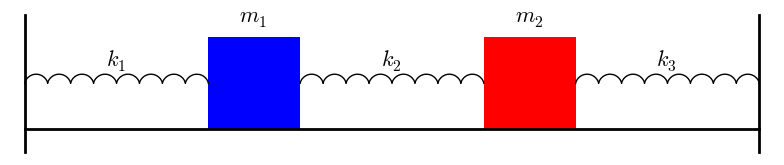
Suppose that the masses are attached to one another and to two immovable walls by means of three identical light horizontal springs of spring constant as shown in Figure 15. Frequencies of a massspring system When the system vibrates in its second mode the equations blbelow show that the displacements of the two masses have the same magnitude with opposite signs. Coupled spring equations TEMPLE H.
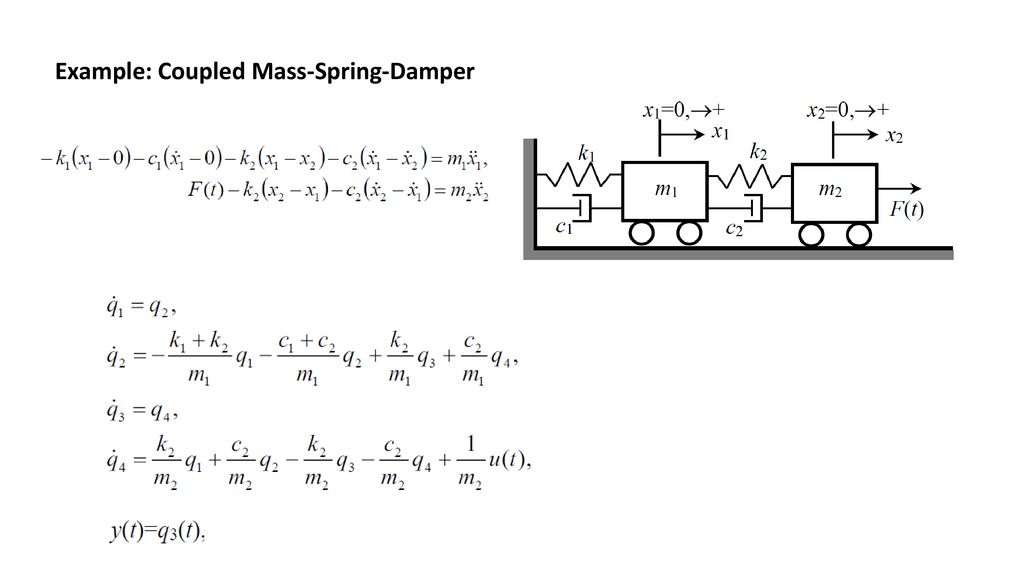
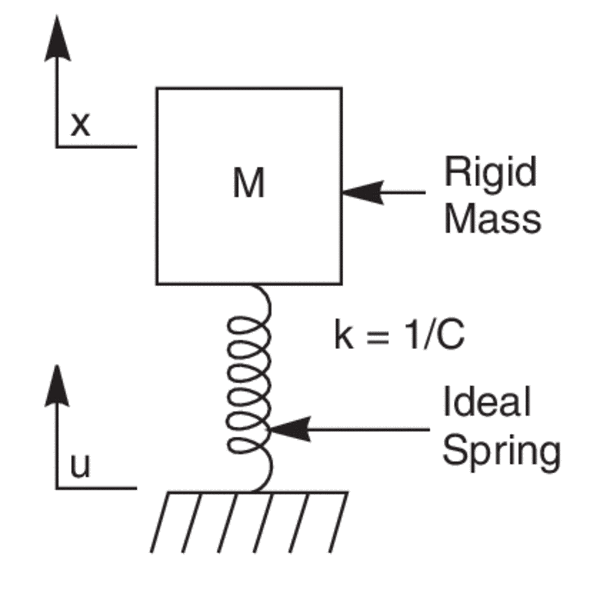
881 Coupled Spring-Mass Systems The motion of a mass attached to the end of a spring was modeled with a second-order linear differential equation with constant coefficients in Chapter 5. Making use of equation 7 and Newtons second and third laws we can write the equations of motion of the masses as M 1 2ξ0t t2 κ0 ξ0t x. Four Masses with with Free Ends without Damping.
Hello I am having trouble trying to find the correct model for this coupled spring system. The scenario is the following we have. The left end of the left spring is fixed.
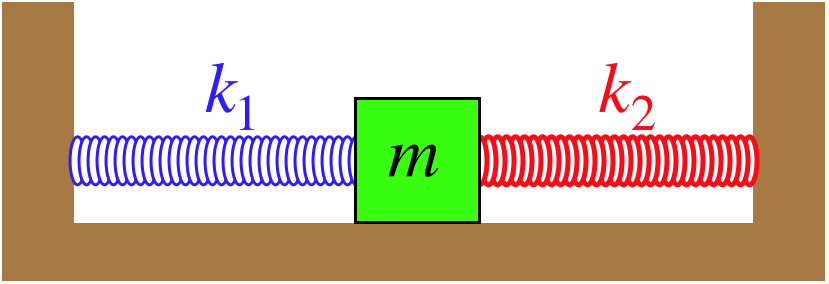
Similarly if a second spring and mass are attached to the end of the first mass then the model becomes that of a system of second-order equations. Clearly the equation for the force on the left mass is identical to the example above Equation 846. For m_1 m_2 and x_1 ne x_2 If I write and solve that EoMs mddotx_1 k_0x_1kx_1 x_2 mddotx_2 -k_0x_2-kx_1x_2 I get omega sqrt4frac2k_0km frack_0m2.
Two Coupled Harmonic Oscillators Consider a system of two objects of mass M. Ic 0 v2_i 0 0. Divide through by the masses to put system 1 in normal form.
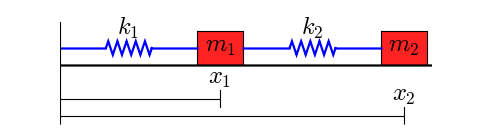
Then its response will be studied and analyzed to calculate the natural frequency of the system. Two objects with masses m 1 and m 2 are coupled through springs with spring constants k 1 and k 2.
Finding the particular integral Then do the same for a.
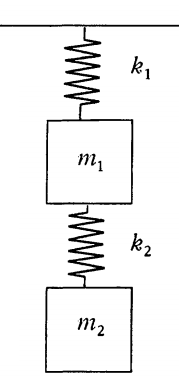
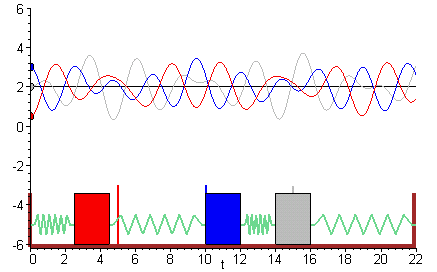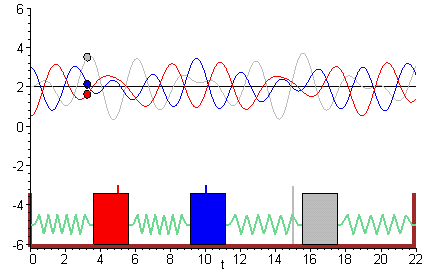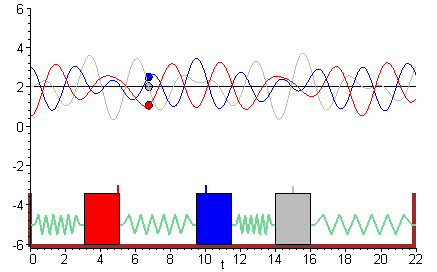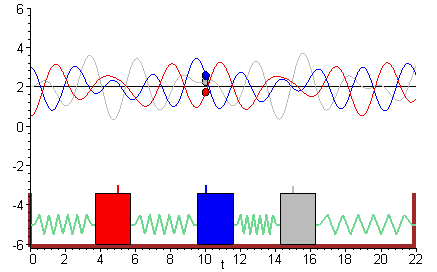
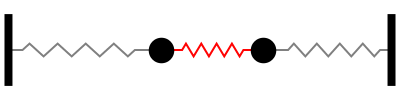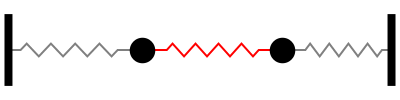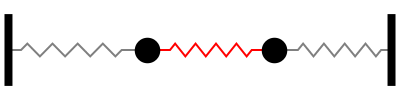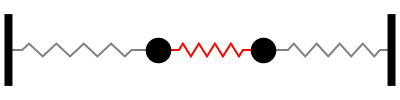
The simplest coupled system 5-1 1 Figure 3A Sloshing modemotion describ ed by the Òslow solution Ó of 7. A Coupled Spring-Mass System. X 1 k 1 x 1 k 2 x 2 x. Particles one of mass M 1 coupled to the left end x 0 of the spring and the other of mass M 2 coupled to the right end x. The two objects are attached to two springs with spring constants κ see Figure 1. Similarly if a second spring and mass are attached to the end of the first mass then the model becomes that of a system of second-order equations. Making use of equation 7 and Newtons second and third laws we can write the equations of motion of the masses as M 1 2ξ0t t2 κ0 ξ0t x. Rather than a single pendulum now let us consider two pendula which are coupled together by a spring which is connected to the masses at the end of two thin strings. Thus the motions of the mass 1 and mass 2 are out of phase.
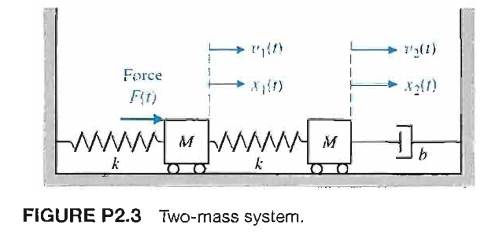
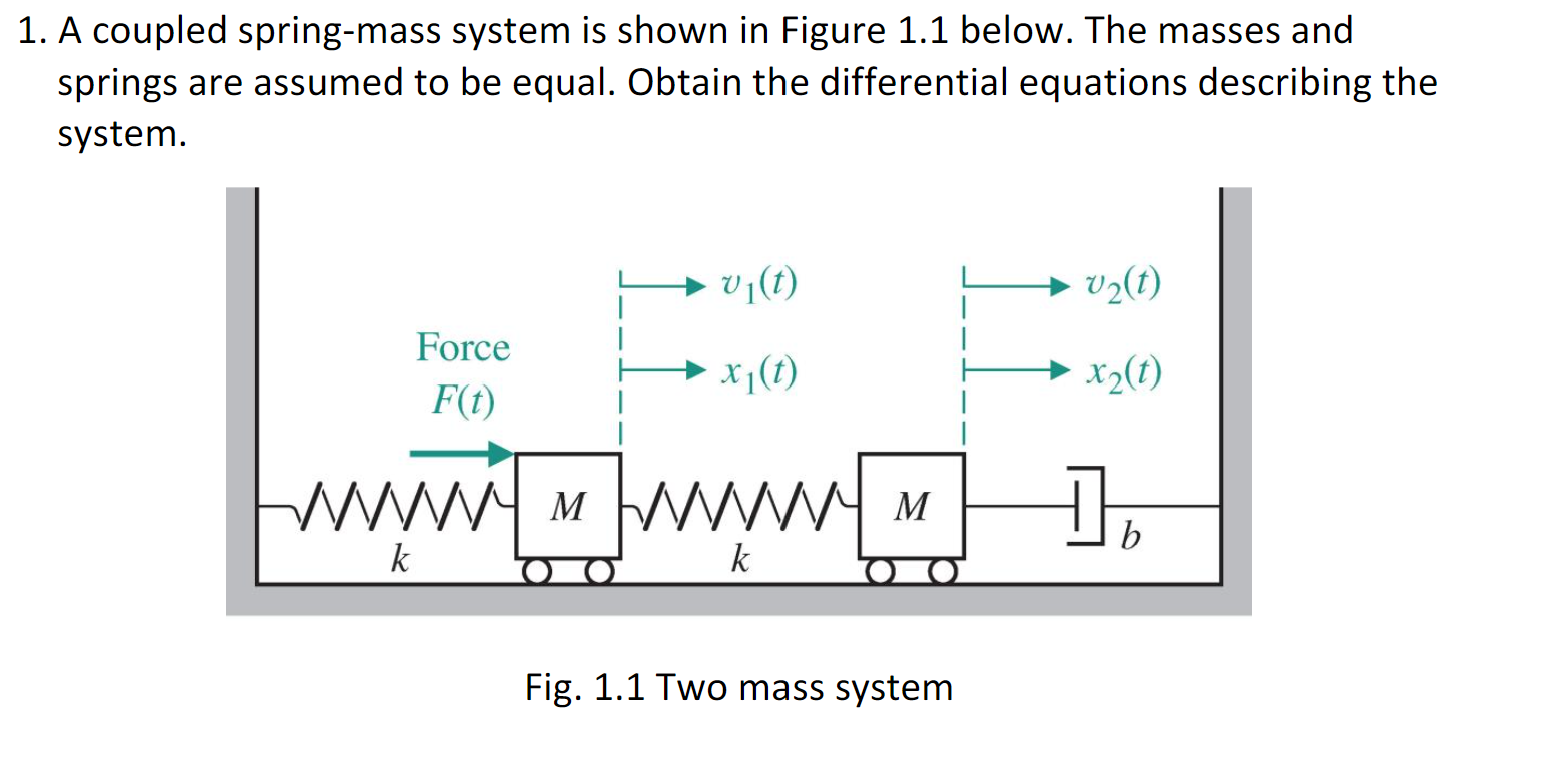
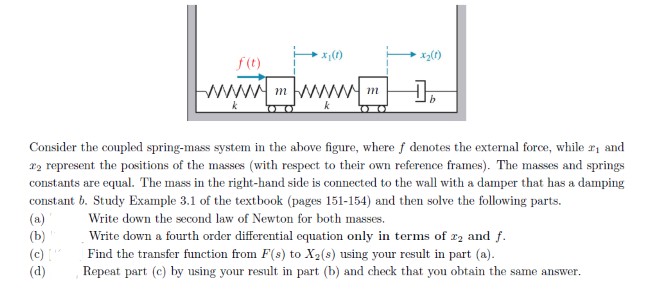
Rather than a single pendulum now let us consider two pendula which are coupled together by a spring which is connected to the masses at the end of two thin strings. Forcing term on mass 2. Similarly if a second spring and mass are attached to the end of the first mass then the model becomes that of a system of second-order equations. So springs with constant k_0 are compressedsprings push masses to their equilibrium then spring with k in mid is stretched pulls the masses to each other. Ceiling - Spring - Mass 1 - Spring 2 - Mass 2 - Spring 3 - Mass 3 End. EXAMPLE 1 The First-Order System that Models Coupled SpringsBlocks. Suppose that the masses are coupled to their immediate neighbors via identical light springs of unstreched length and force constant.





















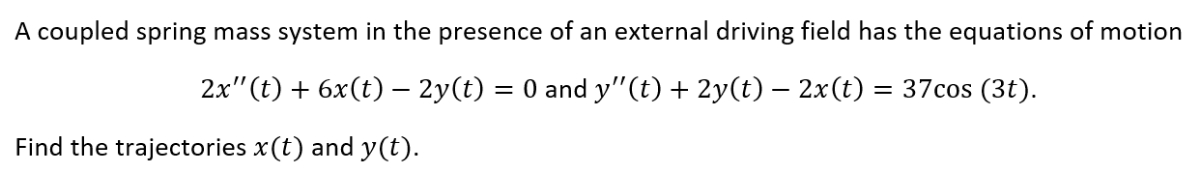
Post a Comment for "Coupled Spring Mass System"